Pengertian dan Cara Mengerjakan RALF (Rancangan Acak Kelompok Faktorial) dengan Cara Manual, Excel, Dan SPSS

Pengertian dan Cara Mengerjakan RALF (Rancangan Acak Kelompok Faktorial) dengan Cara Manual, Excel, Dan SPSS 
RANCANGAN ACAK LENGKAP - FAKTORIAL (RALF)

 1. Penggunaan

Rancangan Acak Lengkap Pola Faktorial AxB adalah rancangan acak lengkap yang
terdiri dari dua peubah bebas (Faktor) dalam klasfikasi silang yaitu faktor A yang terdiri
dari a taraf dan faktor B yang terdiri dari b taraf dan kedua faktor tersebut diduga saling
berinteraksi. Saling berinteraksi dimasudkan bahwa pengaruh suatu faktor tergantung
dari taraf faktor yang lain, dan sebaliknya jika tidak terjadi interaksi berarti berarti
pengaruh suatu faktor tetap pada setiap taraf faktor yang lain. Jadi bila tidak terjadi
interaksi antar taraf-taraf suatu faktor saling sejajar satu sama lainnya, sebaliknya bila ada
interaksi tidak saling sejajar.
    
    2. Pengaturan Unit-unit Penelitian

Prinsip : Semua unit penelitian (perlakuan dan ulangannya) disebar secara acak disatu tempat dan perlakuan terdiri dari 2 atau lebih dari 2 faktor perlakuan
Contoh : 2 taraf  dosis mikoriza dan 3 taraf dosis rizhobium, dengan 3 ulangan.

M₁B₁ (I)
M0B₂ (I)
M₁B₁ (III)
M0B₁ (III)
M₁B₃ (III)
M0B₂ (II)
M0B₃ (I)
M0B₁ (I)
M₁B₂ (III)
M₁B₁ (II)
M₁B₃ (I)
M0B₁ (II)
M₁B₂ (I)
M₁B₂ (II)
M0B₂ (III)
M₁B₃ (II)
M0B₃ (III)
M0B₃ (II)
Gambar 1. Bagan penelitian untuk RALF dua perlakuan, 2 taraf mikoriza dan 3 taraf rizhobium dengan 3 ulangan
 3.  Model Matematika

Hijk = Ļ€ + Pj + Pk + (Pj x Pk) + eijk

Keterangan :
Hijk           = Hasil akibat perlakuan ke-j dan perlakuan ke-k pada ulangan ke-i
Ļ€              = Nilai tengah umum
Pj             = Pengaruh faktor perlakuan ke-j
Pk            = Pengaruh faktor perlakuan ke-k
Pj x Pk    = Interaksi perlakuan ke-j dan perlakuan ke-k
Eijk                    = Eror akibat perlakuan ke-j dan perlakuan ke-k pada ulangan ke-i
i               = 1, 2, …., u (u = ulangan)
j               = 1, 2, …., p ke-1 (p = perlakuan ke-1)
k              = 1, 2,…... p ke-2 (p = perlakuan ke-2)
UNTUK LEBIH JELASNYA PERHATIKAN CONTOH DI BAWAH INI KITA AKAN MENGOLAH DATA DARI HASIL PENELITIAN  INTAN RAHMI (1105104010004), Program Studi Peternakan, Fakultas Pertanian, Universitas Syiah Kuala, 2015, DENGAN JUDUL :KAJIAN SILASE JAGUNG PUTIH DENGAN PERLAKUAN BINOSIL EFEKTIF MIKROORGANISME (EM-4)

Lampiran 2. Protein Kasar
Perlakuan
Ulangan
Jumlah
Rerata
V1
V2
P1
7,06
9,21
16,27
8,14
7,06
9,21
16,27
8,14
7,56
8,51
16,07
8,04
7,56
8,51
16,07
8,04
P2
7,85
8,24
16,09
8,05
7,85
8,24
16,09
8,05
8,11
8,41
16,52
8,26
8,11
8,41
16,52
8,26

129,92
8,12


1.      Faktor Koreksi (FK)  =        (∑yij)2
             (r.a.b)
                                                  =  (129,92)2
         (16)
  =  1054,95
·         Jumlah Kuadrat       
1.      Jumlah Kuadrat  T   =  ∑X2 - FK
               =  {(7,06) 2 + (9,21) 2 + (7,06) 2 +.....(8,41) 2}   - 1054,95
                           =  5,90



2.      JK Perlakuan              = (∑y..) 2/  a.b - FK
                            = {(16,27) 2 + (16,27) 2 + (16,07) 2 +.....(16,52) 2} / 4  –
                        1054,95
                             =   5,07
3.      JKA                               = ∑(a1) 2/ r.b – FK
                             = 0,02
4.      JKB                               = ∑(a1) 2/ r.a – FK
                             = 3,61
5.      JKAB                            = JKP – JKA - JKB
                                       = 5,07 – 0,02 – 3,61
                                       = 1,44
6.      JK Galat                                   = JKT – JKA – JKB – JKAB
     = 5,90 -0,02 – 3,61 – 1,44
                                             =  0,83
·         Derajat bebas
1.      Derajat Bebas (db) Perlakuan              
             = Perlakuan – 1
 =  4 – 1
 = 3
2.      Derajat Bebas (db) A
 = 2 – 1
 =  1
3.      Derajat Bebas (db) B                   
             = 2 – 1
                         = 1
4.      Derajat Bebas (db) AB                   
             = 1 X 1
                         = 1
5.      Derajat Bebas (db) Galat                            
  = ab (r -1 )
  = 12
6.      Derajat Bebas (db) Total                           
Abr – 1 = 15



·         Kuadrat tengah
1.Kuadrat Tengah (KT) Perlakuan             
  = JKP/(p-1)
  =  5,07/ 3
  = 1,69

2. Kuadrat Tengah (KT) A           
 = JKP(A)/(p-1)
 =  0,02/ 1
 = 0,02
     3 Kuadrat Tengah (KT) B    
= JKP(B)/(p-1)
 =  3,61/ 1
 = 3,61
1.      Kuadrat Tengah (KT) AB    
 = JKP(AB)/(p-1)
 =  1,44/ 1
 =  1,44
2.      Kuadrat Tengah Galat                                                      
 = JKG/dbG
     = 0,08/ 12
 = 0,07
·         F Hitung  ( A)   
 = KTA/KTG   
 = 0,02/0,07
 = 0,28
·         F Hitung  ( B)   
 = KTB/KTG   
 = 3,61/0,07
 = 51,57


·         F Hitung  ( AB)   
 = KTAB/KTG   
 = 1,44/0,07
 = 20,57
Tabel Anova :
SK
DB
JK
KT
Fhitung
F Tabel
0,05
0,01
Perlakuan
3
5,07
1,69


A
1
0,02
0,02
0,28  tn
 4,75
 9,33
B
1
 3,61
 3,61
 51,57**
 4,75
 9,33
AB
1
 1,44
 1,44
 20,57**
 4,75
 9,33
Galat
12
 0,83
 0,07



Total
15
5,90




Kesimpulan :
·         Fhitung < Ftabel berarti tidak nyata yaitu  Tidak adanya pengaruh Silase Jagung Putih Dengan Perlakuan Binosil Efektif Mikroorganisme (EM-4).
·         Fhitung >Ftabel berarti berbeda sangat nyata  yaitu   adanya pengaruh Silase Jagung Putih Dengan Perlakuan Binosil Efektif Mikroorganisme (EM-4).
·         Fhitung > Ftabel berarti berbeda sangat nyata yaitu  adanya pengaruh Silase Jagung Putih Dengan Perlakuan Binosil Efektif Mikroorganisme (EM-4).

 
Menganalisis Menggunakan Program Excel
Langkah 1 : Jalankan Program Microsoft Excel
Langkah 2 : Masukkan data Lampiran 1a yang berasal dari Skripsi ke dalam Microsoft Excel
 Langkah 3 : Masukan Rumus untuk mencari rata-rata dan jumlah
Langakah 4. kemudian, untuk mencari jumlah Ulangan (U) hingga ke f hitung gunakan formula seperti di bawah ini dan disesuaikan dengan data yang ada.
Langkah 5. Buat tabel sidik ragamnya dengan formula dibawah ini, sesuaikan dengan data.
KESIMPULAN : Fhitung < Ftabel berarti tidak nyata yaitu  Tidak adanya pengaruh Silase Jagung Putih Dengan Perlakuan Binosil Efektif Mikroorganisme (EM-4)
Menganalisis Menggunakan Program SPSS
Ketika membuka Program SPSS, ada dua Windows yang muncul yang pertama Untuk Data dan yang kedua yaitu Untuk Output setelah menganalisis
Ƙ  Tampilan Bagian Data

Langkah 2 : Mengisi bagian Varibel view seperti di bawah ini
Klik bagian perlakuan pada values untuk memberikan label perlakuan1 dan perlakuan2 yang akan kita buat.Selanjutnya klik bagian kelompok pada values untuk memberikan label pada kelompok yang kita lakukan.
Mengisi data view
 Selanjutnya Isi Bagian Kolom Perlakuan1 dan perlakuan2, ulangan, dan Hasil. Seperti di bawah ini.
 
Menganalisis Data
Klik Bagian Analyze General Linear Model  Univariate
Setelah itu muncul, Klik Bagian [Hasil] Klik Tanda Panah Pada Bagian Dependent Variable,
Setelah itu Klik protein kasar silase  Bagian Ulangan  Klik tanda panah pada bagian Fixed Factors, tapi melakukannya satu persatu, lalu muncul seperti ini :
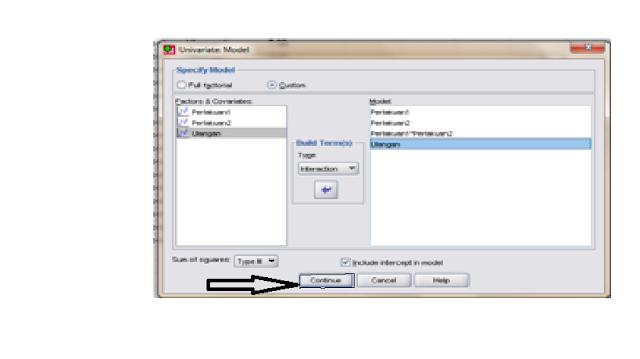
Klik Bagian Model Klik Custom,Setelah diklik Model, Setelah itu tampil Kotak dialog yang baru, lalu klik continue seperti di bawah ini:
 Klik bagian Post Hoc, Post Hoc berfungsi untuk menguji Lanjut dari Hasil Penelitian
 Setelah itu tampil Kotak dialog yang baru,Klik Bagian Perlakuan 1, dan perlakuan 2,
Setelah itu Klik Bagian LSD (untuk Uji BNJ), Tukey (untuk Uji BNJ), dan Duncan (Untuk Uji Duncan)  Klik Continue,
klik ok maka akan muncul tampilan :
setelah itu ,keluar output dari spss
uji lanjut dari data diatas adalah





Referensi : http://syarifahrenny.blogspot.co.id/2014/05/rancangan-acak-lengkap-faktorial-ralf_5.html
Nama : Annisa Wahyuni
Nim   : 1405104010015

 

Komentar

  1. Telkom University27 Februari 2024 pukul 22.56

    Apa yang membedakan pola faktorial AxB dengan Rancangan Acak Lengkap biasa? Kunjungi Kami Telkom University

    BalasHapus

Posting Komentar

Postingan populer dari blog ini

CARA MENGANALISIS RAL SECARA PERHITUNGAN MANUAL,EXCEL, DAN SPSS

Gambar
CARA MENGANALISIS RAL SECARA PERHITUNGAN MANUAL,EXCEL, DAN SPSS   MENGGUNAKAN RAL SECARA PERHITUNGAN Rancangan Acak Lengkap (RAL) Suatu percobaan yang digunakan homogen atau tidak ada fakt or lain yang mem peng aruhi resp on di luar faktor  yang diteliti. Pada rancangan acak lengkap (RAL) digunakan jika kondisi unit percobaan yang digunakan relatif homogen. Penerapan perlakuan terhadap unit percobaan dilakukan secara acak terhadap seluruh unit percobaan. Seperti percobaan-percobaan yang dilakukan di laboratorium atau rumah kaca yang pengaruh lingkungannya lebih mudah dikendalikan. Rancangan acak lengkap dipergunakan jika variabel luar tidak diketahui, atau bila pengaruh variabel ini yang sengaja tidak dikontrol terhadap variasi subyek, adalah sangat kecil. Rancangan ini juga dipakai jika diketahui bahwa subyek keadaannya seragam dan inferensi yang dibuat berdasarkan hasil percobaan tidak dimaksudkan sebagai inferensi yang bersifat percobaan tidak d...
Baca selengkapnya

CARA MENGANALISIS RAK SECARA PERHITUNGAN MANUAL,EXCEL, DAN SPSS

Gambar
C ARA MENGANALISIS RAK SECARA PERHITUNGAN MANUAL,EXCEL, DAN SPSS MENGGUNAKAN RAK SECARA MANUAL    Rancangan Acak Kelompok adalah suatu rancangan acak yang dilakukan dengan mengelompokkan satuan percobaan ke dalam grup-grup yang homogen yang dinamakan kelompok dan kemudian menentukan perlakuan secara acak di dalam masing-masing kelompok. Rancangan Acak Kelompok Lengkap merupakan rancangan acak kelompok dengan semua perlakuan dicobakan pada setiap kelompok yang ada. Tujuan pengelompokan satuan-satuan percobaan tersebut adalah untuk membuat keragaman satuan-satuan percobaan di dalam masing-masing kelompok sekecil mungkin sedangkan perbedaan antar kelompok sebesar mungkin. Tingkat ketepatan biasanya menurun dengan bertambahnya satuan percobaan (ukuran satuan percobaan) per kelompok, sehingga sebisa mungkin buatlah ukuran kelompok sekecil mungkin. Pengelompokan yang tepat akan memberikan hasil dengan tingkat ketepatan yang lebih tinggi dibandingkan ranca...
Baca selengkapnya